| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 데이터
- MAE
- 정보화진흥원
- 1D CNN
- edge computing
- CNN
- Data Imbalance
- 머신러닝
- nvidia
- 공부
- 빅데이터
- GE B650
- 회귀
- R
- 데이터불균형
- VitalDB
- 딥러닝
- 회귀분석
- 데이터분석
- 2D CNN
- VitalRecorder
- 엣지컴퓨팅
- 경진대회
- NIA
- 생체신호
- 알고리즘
- 의료데이터
- 나이브베이즈
- Undersampling
- Jetson
- Today
- Total
Doyun-lab
[ML] Data Imbalance (불균형 데이터 분석을 위한 방법들) 본문
앞선 포스팅에서 다뤘듯이 불균형 데이터 문제를 해결하기 위한 방법에는 여러가지가 있습니다.
불균형 데이터 문제 해결을 위해 여러가지 자료를 탐색하던 중 좋은 강의가 있어 그것을 참고하여 정리해봤습니다 !
고려대학교 인공지능공학연구소 김성범 소장님의 "불균형 데이터 분석을 위한 샘플링 기법" 강의를 추천해주고 싶습니다.
저작권에 문제가 된다면, 언제든지 연락주시면 해당 포스팅을 삭제 조치 하겠습니다.
이번 포스팅에서는 불균형 데이터 문제를 해결하기 위한 여러가지 방법에 대해서 다뤄보려고 합니다.
불균형 데이터일 경우 무엇이 문제인가 ?
일반적인 경우에 이상(소수)을 정확히 분류하는 것이 중요한데, 이상(소수)을 정확히 찾아내지 못한다.
이 경우 정확도는 높게 보이지만 이상(소수)에 관한 분류 성능은 좋지 않을 수 있다. 여기서 모델 성능에 대한 왜곡이 생길 수 있는 것이 문제점이다.
불균형 데이터의 대표적인 해결방안
1. 데이터를 조정해서 해결 ⇒ Sampling 기법'
2. 모델을 조정해서 해결 ⇒ 비용 기반 학습(Cost sensitive learning), 단일 클래스 분류 기법(Novelty detection)
이번 포스팅에서는 첫번째와 두번째 방법 중에 첫번째 방법인 Sampling 기법에서 자세히 다뤄보겠습니다.
샘플링 기법
샘플링 기법에는 Under-sampling과 Over-sampling이 있습니다. 앞선 포스팅에서 Down-sampling과 Up-sampling의 유사한 개념인데요. 이 두 가지 Sampling 기법에도 여러가지 방법이 있습니다.

1. Under-sampling
- Random Under-sampling
다수 Class에 속해있는 관측치를 줄이는 방법입니다. 다수 Class에서 무작위로 Sampling을 하여 줄이게 되는데요. 무작위로 Sampling을 하기 때문에 할 때 마다 다른 결과가 나오는 것이 단점입니다. 이 방법은 정말 단순한 방법이지만 적용해보면 의외로 좋은 결과가 도출됩니다.
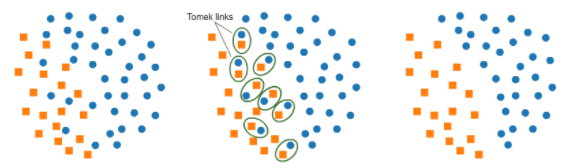
- Tomek Links
두 Class 사이를 탐지하고 정리를 하여 부정확한 분류 경계선을 방지하는 것입니다. 적용 방식은 먼저 Tomek Links를 형성한 후 다수 Class에 속한 관측치를 제거하는 방법입니다. Tomek Links를 형성하는 방법은 두 개의 다른 Class를 선으로 이었을 때, 두 Class 중간에 다른 관측치가 없는 경우 Link를 형성하게 됩니다. 아래의 그림처럼 두 개의 다른 Class가 Tomek Links 된 것을 볼 수 있습니다.
- Condensed Nearest Neighbor Rule (CNN)
소수 Class 전체와 다수 Class에서 무작위로 하나의 관측치를 선택하여 Sub Data를 구성합니다. 1-Nearest Neighbor(1NN) Algorithm을 통해 원 데이터를 분류하고 정상 분류된 다수 Class 관측치를 제거합니다. 여기서 고려해야할 점은 무조건 1-NN Algorithm을 사용해야 한다는 것입니다. 만약, k = 3 으로 설정하고 3-NN을 실시했을 경우 Sub Data에서 정상 Class가 하나만 선택되어 있기 때문에 모든 데이터가 이상으로 분류되는 문제가 발생합니다.
아래 그림을 보면 다수 Class가 상당히 제거 되고 초록색 Data와 기존에 선택된 하나의 관측치만 남게 됩니다.


- One-sided Selection
이는 Tomek Links와 CNN을 모두 적용한 것이라고 생각하면 됩니다. Tomek Links와 CNN을 통해 제거된 부분을 모두 지우는 방법입니다. 이를 적용하면 CNN을 적용한 데이터에 소수 Class에 가까운 경계선 부분이 제거된 후 다수 Class들이 남게 됩니다.
- Under-sampling의 장단점
장점 : 다수 Class 관측치 제거로 인한 계산 시간 감소, Class overlab 감소
단점 : 데이터 제거로 인한 정보 손실 발생 (제거한 것이 분류에 큰 영향을 끼치는 데이터일 수 있음 !)
2. Over-sampling
- Resampling
소수 Class 내 관측치를 단순히 증폭시키는 방법입니다. 즉, 소수 Class를 Copy 한다고 생각하면 됩니다. 이 방법을 사용하게 되면 소수 Class에 과적합이 발생할 가능성이 있습니다.
- SMOTE (Synthetic Minority Over-sampling Technique)
소수 Class에서 가상의 데이터를 생성하는 방법입니다.
생성하는 방법은 먼저 k를 정합니다. 예를 들어 k를 5로 설정했다고 한다면 소수 Class에서 임의로 하나의 관측치를 선택하고 주위에 제일 가까운 5가지를 선택합니다. 그 5개 중 랜덤하게 하나의 관측치를 선택합니다. 그 후, 소수 Class에서 임의로 선택된 관측치와 가까운 5가지 중 랜덤하게 선택된 하나의 관측치의 차이를 계산한 후 소수 Class에서 임의로 선택된 관측치에 0 ~ 1 사이의 값을 랜덤하게 곱해줍니다. 이는 소수 Class에서 임의로 선택된 관측치를 랜덤하게 선택된 하나의 관측치로 특정 값만큼 이동시키는 것을 의미합니다.
이런 방식으로 새로운 데이터를 생성해줍니다. 지금까지의 과정을 모든 소수 Class 관측치에 대해 반복하여 가상 관측치를 생성합니다. 여기서 주의해야할 점은 k ≥ 2 (k ≠ 1)이어야만 합니다. k가 1일 경우 두 점 사이에 쭉 늘어진 형태의 데이터가 생성되므로 주의해야 합니다.

X : 소수 Class에서 임의로 선택한 관측치 / nn : Nearest neighbor 관측치 중 랜덤하게 하나 선택한 것
u : Uniform Distribution [unif(0, 1)] / Synthetic : 새로 생성된 관측치

- Borderline-SMOTE
Borderline(경계) 부분만을 샘플링을 하는 방법입니다. 경계 부분에서 멀어진 부분에 데이터가 생성이 된다고 하더라도 큰 도움이 되지 않는다는 아이디어에서 이러한 알고리즘이 도출되었습니다. 정상 Class와 소수 Class가 많은 부분에 데이터가 많아야 추후 분류 모델을 만들 때 도움이 되기 때문인데요.
작동하는 방식은 먼저 Boderline을 찾습니다. Boderline을 찾는 방법은 소수 Class xi에 대해 k개 주변을 탐색하여 k개 중 다수 Class(정상 Class)의 수를 확인합니다. 여기서 k를 5로 예로 들자면, 다수 Class 수가 0이면 Safe 관측치. 다수 Class 수가 3이면 Danger 관측치 (Borderline 이라는 뜻). 다수 Class 수가 5이면 Noise 관측치라고 합니다.
이러한 기준을 식으로 나타내면,
k = 소수 Class 주변 탐지 관측치의 수
k' = k 소수 Class 주변의 다수 Class 수
Noise 관측치 : k = k'
Danger 관측치 : k/2 < k' < k
Safe 관측치 : 0 ≤ k' ≤ k/2
이 과정을 거친 후에 Danger 관측치에 대해서만 SMOTE Algorithm을 적용합니다. 이렇게 적용을 하게되면 전반에 걸쳐 Sample이 생성되는 것이 아니라 경계선 주위만 Sample이 생성됩니다. 여기서 핵심은 새로 생선된 데이터들이 경계선에 생긴다는 것입니다.

- ADASYN (Adaptive Synthetic Sampling Approach)
Sampling 하는 개수를 위치에 따라 다르게 하는 방법입니다. 먼저 아래의 식에 대해 이해하는 시간을 갖겠습니다.

Δi : 소수 Class xi의 주변 K개 중 다수 Class 관측치 수
m : 소수 Class 내 관측치 총 개수
위의 식은 각 소수 Class 주변에 얼만큼 많은 다수 Class 관측치가 있는가를 정량화 한 지표입니다.
모든 소수 Class에 대해 주변을 k개만큼 탐색하고 그 중 다수 Class 관측치의 비율을 계산 합니다. 이 과정이 ri를 구하는 과정입니다. 계산한 ri를 scaling 해줍니다. scaling은 ri를 전부 다 더한 뒤 더한 값으로 나눠줍니다. scaling 한 후, 생성하고자 하는 개수만큼 곱합니다. 여기서 ri의 정도에 따라 생성되는 Sample의 수가 달라집니다.
모든 ri 값에 G(생성하고자 하는 개수)만큼 곱하여 생성되는 소수 Class 수를 구합니다. 소수 Class 주변의 다수 Class 수에 따라 유동적으로 Over-sampling 개수를 결정합니다. Sample은 각 소수 Class를 seed로 하여 할당된 개수 만큼 SMOTE를 적용하여 생성합니다.
ADASYN은 Borderline뿐만 아니라 다수 Class 쪽에 있는 소수 Class에 더 집중해보자는 아이디어에서 도출된 것입니다. 또한, 다수 Class의 데이터가 패턴이 다수인 경우에 잘 작동하는 모습을 보입니다.

- Over-sampling의 장단점
장점 : 정보 손실이 없다, 대부분의 경우 Under-sampling에 비해 높은 분류 정확도
단점 : 과적합 가능성, 계산 시간 증가, Noise 또는 이상치에 민감
비용 기반 학습 (Cost Sensitive Learning)
이는 오분류 비용이 같을까 ? 라는 질문에 대해 생각해보면 쉽게 이해할 수 있습니다. 아래의 예시를 보신다면,
1. 이상(소수)을 정상(다수)으로 분류
2. 정상(다수)을 이상(소수)으로 분류
위의 두 예시 중 무엇이 더 치명적일까요 ? 바로 1번이 더 치명적입니다. 즉, 오분류 비용이 다르다는 것입니다. 비용 기반 학습은 모델링에 오분류 비용을 고려하는 것인데요. 비용 기반 데이터에 가중치를 부여하여 작동합니다. 쉽게 말하면 각 Class에 다른 오분류 비용을 부여하여 분류기를 생성하는 것입니다.
만약 오분류 비용을 정상 : 이상 = 1 : 10 으로 했다면, 이상에 비용을 10배를 준 것인데 이는 이상인데 정상으로 하는 경우에 더 가중치를 준 것입니다. 이상인데 정상으로 분류하지 못하도록 말이죠.
정리하자면, 비용(Cost)에 기반하여 비용이 높은 Class 일수록 그 Class를 분류하는 데 더욱 집중하여 학습하는 것입니다.
단일 클래스 분류 기법 (Novelty detection)
이는 가능한한 모든 다수 Class를 포함하는 분류 경계선을 생성하는 기법입니다. 중심을 기준으로 다수 Class를 잘 설명하는 Boundary를 생성하는 것입니다. 대표적인 Algorithm으로 Support Vector Data Description (SVDD)가 있습니다.
'Study > Machine Learning' 카테고리의 다른 글
| [ML] Data Imbalance Problem (데이터 불균형 문제) (0) | 2021.06.24 |
|---|---|
| [ML] Perceptron (퍼셉트론) (0) | 2021.06.21 |
| [ML] SVD / PCA / LDA (0) | 2021.06.21 |
| [ML] Naive Bayes (나이브 베이즈) (0) | 2021.06.21 |
| [ML] Decision Tree (의사결정 나무) (0) | 2021.06.21 |




